■三本の矢は一本の矢の何倍強いか　〜三矢の訓とサンフレッチェ広島〜

[ 改訂：2014/10/01　断面2次モーメントの計算式に一部誤りがあり、修正しました（本文末尾参照）。]

　戦国武将の毛利元就（もうりもとなり、1497-1571）が３人の息子に
　　「１本の矢なら折れるが、３本の矢なら折れない」
と戒めた「三本の矢」の逸話（三矢の訓： さんしのおしえ）は、あまりにも有名ですが、同じような話は世界中に残されているようです。

　１本の矢より３本の矢の方が折れにくい（強い）ことは明らかですが、では一体何倍の強度なのでしょうか。

　単純には３倍と思われますが、実は構造材に負荷を加えたときの変形や破壊について研究する学問である「材料力学」の理論をもとに計算すると何と １本の矢の約５倍の強度（折れにくさ） になることがわかります。
　また「たわみにくさ」については、１本の矢の約１１倍 にもなるのです。

　うまく組み合わせる（協力する）ことによって単純に3倍でなく、それ以上の力を発揮する訳です。

　Jリーグ：サンフレッチェ（SANFRECCE）広島の「サンフレッチェ」の名称はこの「三矢の訓」に因んで付けられたもので、日本語の「三（サン）」とイタリア語で「矢」を表す「フレッチェ」を合わせた造語なのです。　選手一丸となって更なる躍進を期待したいところです。



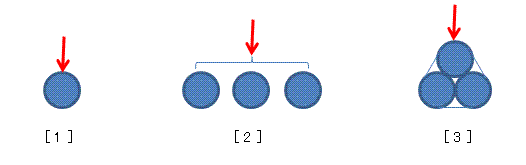
　参考までに、「三本の矢」のたわみと強度の計算過程を示します。

　横荷重を受ける細くて長い棒状のもの（梁という）のたわみの量は、次式で定義される断面形状に関する断面2次モーメント：Iに反比例します。

　　I　＝　Σy²ΔA = ∫ y²dA
　ここで、
　　y　　　　：　断面の図心からの距離
　　ΔA,　dA：　微小面積

　図の（１）、（２）、（３）の各形状の断面2次モーメントはそれぞれ次のようになります。

（１）断面が直径ｄの円形１個の場合
　　　I₁ = πd⁴/64

（２）断面が直径ｄの円形３個を単純に横に並べた場合
　　この場合は単純に（１）の3倍で
　　　I₂ = I₁*3 = πd⁴/64*3

（３）断面が直径ｄの円形３個を図のように強固に束ねた場合
　　この場合の図心位置が下側の２つの円形の中心を結ぶ線から上方に ec：
　　　ec = d/(2√3)
　　だけずれることを考慮して計算すると、
　　　I₃ = πd⁴/64*( 3 + 8/3 + 16/3 )　 [ ＜−＞ 修正前は 　　I₃ = πd⁴/64*( 3 + 8/3 + 16/√3 ) ]

　　∴ I₃ ＝ I₁ * 11
　となり、たわみは円形３個を単純に横に並べた（２）の場合の約１／４、円形１個の場合の１／１１となります。

　細くて長い棒状のもの（梁）の強度すなわち折れにくさは、次式で定義される断面形状に関する断面係数：Zに反比例します。

　　Z　＝　I / e0
　ここで、
　　I ：　断面２次モーメント
　　e0：　断面の図心位置から断面の上端または下端までの距離の大きい方

　図の（１）、（２）、（３）の各形状に対してはそれぞれ次のようになります。

（１）断面が直径ｄの円形１個の場合
　　　e0 = d/2
　　　Z₁ = I₁/e0 = πd³/32

（２）断面が直径ｄの円形３個を単純に横に並べた場合
　　　e0 = d/2
　　　Z₂ = I₂/e0
　　　　　= Z₁*3

（３）断面が直径ｄの円形３個を図のように強固に束ねた場合
　　図心位置から断面下端までの距離 e1：
　　　e1 = ec + d/2 = d/2*(1+1/√3)
　　図心位置から断面上端までの距離 e2：
　　　e2 = (√3/2)d - ec + d/2 = d/2*(1+√3-1/√3)
　　e1 ＜ e2 であるので、
　　　e0 = e2 = d/2*(1+√3-1/√3) ≒ 1.077 d

　　従って、
　　　Z₃ = I₃/e0
　　　　 ≒ I₁*11 / (1.077d)
　　　　 ≒ πd⁴/64*11 / (1.077d)
　　　　 ≒ Z₁*11 / 1.077 / 2

　　∴ Z₃ ≒ Z₁ * 5.11
　となり、強度は円形３個を単純に横に並べた（２）の場合の約１．７倍、円形１個の場合の約５倍となります。


[ 2014/10/01の改訂について ]
　断面が直径ｄの円形３個を上図のように強固に束ねた場合の断面2次モーメント I₃の計算式：

　　I₃ = πd⁴/64 + πd²/4・[ √3/2・d - ec ]² + [ πd⁴/64 + πd²/4・ec² ]・2

　に、図心位置 ec = d/(2√3) を代入して整理すると

　　I₃ = πd⁴/64・3 + πd²/4・[ 2d²/12 + d²(1/√3)² ]
　　　　= πd⁴/64・[ 3 + 16/3 + 8/3 ]
　　　　= πd⁴/64・11

　となります。

　改訂前は上記赤字の2乗処理が落ちていました。

[ 2014/10/07 追記 ]
　ここでは3本の矢は強固に束ねられ、一体として変形すると仮定しています。
　これに対して、3本の矢がそれぞれ独立に変形すると仮定すると、その強度等は上図[2]の場合と同等となります。