丂丂丂乽GPS娙堈僔儈儏儗乕僔儑儞僾儘僌儔儉乿
偵偍偄偰丄怓乆側帪崗偱偺埵抲専弌傪帋傒傞偲帪乆乽岆嵎夁戝乿偑敪惗偡傞偙偲偑偁傝傑偡丅偙偺僾儘僌儔儉偱偼岆嵎乮抧昞偐傜偺崅偝曽岦嫍棧乯偑10km傪挻偊傞偲偙偺儊僢僙乕僕偑弌椡偝傟傑偡偑丄側偤偙偺傛偆側戝偒側岆嵎偑敪惗偡傞偺偱偟傚偆偐丅
丂庴怣婡撪憼偺帪寁偺岆嵎偼僾儘僌儔儉偺弶婜愝掕偱偼俁兪s(昐枩暘偺俁昩)偵愝掕偝傟偰偄傑偡乮夋柺憖嶌偱曄峏壜擻乯偺偱丄嫍棧偵偟偰
丂丂嚈倰丂亖丂俁侽枩km/s x 3兪s = 30x104 x 3x-6 = 0.9km
掱搙偺岆嵎偱偡丅俁偮偺塹惎傪拞怱偲偡傞偦傟偧傟偺媴柺偺敿宎偑嚈倰偩偗憹壛乮偁傞偄偼尭彮乯偟偨帪偵丄俁媴柺偺岎揰嵗昗偑偄偔傜曄壔偡傞偐傪峫嶡偟偰傒傑偟傚偆丅
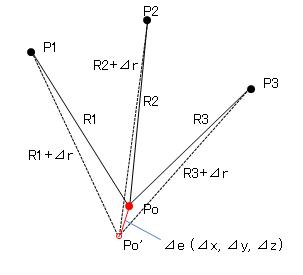
丒Pi(Xi, Yi, Zi),i=1,2,3 傪奺塹惎偺埵抲丄Po(Xo, Yo, Zo)傪庴怣婡偺埵抲偲偟丄塹惎偲庴怣婡偲偺嫍棧傪 丂Ri(i=1,2,3)偲偟傑偡丅 丒偡傞偲師幃偑惉傝棫偪傑偡丅 丂丂Ri2 =乮Xi-Xo)2 + (Yi-Yo)2 + (Zi-Zo)2丂(i=1,2,3)丂丒丒丒(幃侾) 丒敿宎岆嵎乮嫍棧偺岆嵎乯嚈倰偵傛傞岎揰嵗昗岆嵎傪乮嚈x, 嚈y, 嚈z乯偲偡傞偲丄乮幃侾乯傛傝乮旝暘偟偰乯 丂丂Ri嚈倰 = 乮Xo-Xi)嚈x + (Yo-Yi)嚈y + (Zo-Zi)嚈z丂(i=1,2,3)丂丂丂丂丂丂丂丒丒丒(幃俀乯 丂丂嚈倰 = 乮[Xo-Xi)/Ri]嚈x + [(Yo-Yi)/Ri]嚈y + [(Zo-Zi)/Ri]嚈z丂(i=1,2,3)丂丒丒丒(幃俀乫) 丂塃曈偼扨埵儀僋僩儖[Xo-Xi)/Ri, (Yo-Yi)/Ri, (Zo-Zi)/Ri]偲岆嵎儀僋僩儖[嚈x,嚈y,嚈z]偺撪愊備偊丄 丂椉幰偺側偡妏傪兤i丄岆嵎儀僋僩儖偺戝偒偝傪嚈e偲偡傞偲 丂丂嚈倰 = 嚈e丒cos兤i (i=1,2,3) 丂丒丒丒(幃俁乯 丒(幃俁乯偱丄嚈倰丄嚈e偼奺塹惎偵嫟捠偱偁傝丄廬偭偰妏兤i 傕奺塹惎偵嫟捠偺抣偲側傝傑偡丅 丂偡側傢偪丄岆嵎儀僋僩儖偼奺塹惎偲庴怣婡傪寢傇俁儀僋僩儖乮慄暘乯偵懳偟偰摨偠妏搙偲側傝傑偡丅 丒(幃俀乯偺俁尦楢棫曽掱幃傪夝偔偲乮嚈x, 嚈y, 嚈z乯偑媮傔傜傟傑偡丅 丂丂R1嚈倰 = 乮Xo-X1)嚈x + (Yo-Y1)嚈y + (Zo-Z1)嚈z 丂丂R2嚈倰 = 乮Xo-X2)嚈x + (Yo-Y2)嚈y + (Zo-Z2)嚈z 丂丂R3嚈倰 = 乮Xo-X3)嚈x + (Yo-Y3)嚈y + (Zo-Z3)嚈z丂 丂偡側傢偪丄 丂丂 丂丂乥乮R1嚈倰) (Yo-Y1) (Zo-Z1)乥 丂丂 丂丂乥乮R1嚈倰) (Yo-Y2) (Zo-Z2)乥 丂丂 丂丂乥乮R1嚈倰) (Yo-Y3) (Zo-Z3)乥 丂丂嚈x = 乗乗乗乗乗乗乗乗乗乗乗乗乗乗 , 嚈y = 乧, 嚈z = 乧乮摨條乯 丂丂 丂丂乥 乮Xo-X1) (Yo-Y1) (Zo-Z1)乥 丂丂 丂丂乥 乮Xo-X2) (Yo-Y2) (Zo-Z2)乥 丂丂 丂丂乥 乮Xo-X3) (Yo-Y3) (Zo-Z3)乥 丂偙偙偱暘曣偺峴楍幃偼儀僋僩儖 V1(P1Po), V2(P2Po), V3(P3Po)偺僗僇儔乕俁廳愊 V1丒(V2xV3)偱偁傝丄 丂V1,V2,V3偑摨堦暯柺撪偵偁傞偲偒偼奜愊(V2xV3)偲V1偑捈岎偟丄暘曣亖侽偲側傝傑偡丅 丂廬偭偰丄偙傟傜俁儀僋僩儖偑傎傏摨堦暯柺撪偵偁傞偲偒偼乮嚈x,嚈y,嚈z乯偑旕忢偵戝偒偔側傝丄岎揰嵗昗 丂偑杮棃偺埵抲偐傜戝偒偔偢傟傞偙偲偵側傝傑偡丅 丒偙偺偙偲偼(幃俁乯偐傜傕抦傞偙偲偑偱偒傑偡丅 丂俁塹惎偲庴怣婡偑摨堦暯柺忋偵偁傞応崌傪峫偊傑偡丅偙偺帪丄岆嵎儀僋僩儖偼偙偺暯柺偵悅捈側曽岦偵側傝傑偡丅 丂廬偭偰兤i = 90亱丄cos兤i = 亣偲側偭偰丄(幃俁)傛傝嚈e偑嬌抂偵戝偒偔側傝傑偡丅偙傟偑乽岆嵎夁戝乿偺尨場偱偡丅 丒崱夞偺僾儘僌儔儉偱偼庴怣壜擻塹惎偐傜幚嵺偵埵抲寁嶼乮應埵乯偵巊梡偡傞塹惎傪柍嶌堊偵俁屄慖掕偟偰偄傑偡偺偱丄 丂偙偺傛偆側尰徾偑偍偙傝傑偡丅 (拲乯幚偼橂妏乮兝乯傪90搙偵愝掕偡傞偲丄埲屻忋婰偺忬懺傪偱偒傞偩偗夞旔偡傞張棟偑峴傢傟丄埵抲岆嵎偺憹戝傪 丂丂梷偊傞傛偆偵側偭偰偄傑偡丅