■人工衛星の軌道に関する運動方程式

　人工衛星の打上げシミュレーションプログラム "iEarth Satellite"では大気の摩擦を無視し、人工衛星には地球との間の引力しか作用しない（二体問題）として次の万有引力の法則をベースに運動方程式を構成し、これを解いて軌道を計算しています。
　　F = GMm / r²
　ここで、
　　　F　：　万有引力の大きさ
　　　G　：　万有引力定数 (＝6.67259x10^-11 m³s^-2kg^-1)
　　　M　：　地球の質量 (＝5.9742x10²⁴ kg)
　　　m　：　人工衛星の質量
　　　r　：　地球の中心と人工衛星の距離


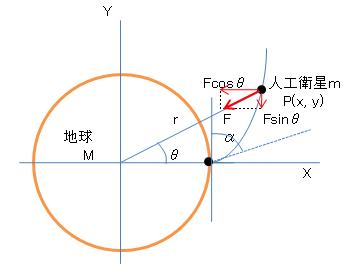
さて、図のように座標系を設定して人工衛星ｍの運動方程式：ｍａ＝Ｆ（ａ：加速度）をｘ、ｙ軸成分に分解して表現すると、
　　mx”＝　−Ｆcosθ　＝　-GMm/r²・x/r　＝　-GMmx/r³
　　my”＝　−Ｆsinθ　＝　-GMm/r²・y/r　＝　-GMmy/r³
整理して、
　　x”＝　-GMx/r³
　　y”＝　-GMy/r³
　ここで、r² = x² + y²

この連立微分方程式を初期条件［時刻t=0 で x=r0, y=0, 速度v=v0］のもとで解けば人工衛星の軌道が求められます。打上げ角度をαとすると、初期条件［時刻t=0 で速度v=v0］は［時刻t=0 で x'=v0sinα、y'=v0cosα］となります。

（注１）x"、y" はそれぞれ時刻ｔに関する2階の導関数（加速度）です。
（注２）初期条件［時刻t=0 で x=r0］について
　　　地表から打上げる場合は r0 は地球の半径、また航空機など上空からの打上げ時は地球の半径＋高度となります。
（注３）第一宇宙速度、第二宇宙速度について
　・人工衛星を地球を周回する円形軌道に乗せるための速度を第一宇宙速度V1といいます。
　　　計算式：　V1 = (GM/r)1/2
　　従って、地球すれすれに回る人工衛星では r = 6,370,000 m として V1≒7.9km/sとなります。
　　第一宇宙速度V1は次の式でも計算できます（mg = GMm/r2 より）。
　　　別の計算式：　V1 = (gr)1/2　、ここで g = 9.8 m/s2 (重力加速度)
　・人工衛星が地球の重力圏から脱出するための速度を第二宇宙速度V2といいます。
　　　計算式：　V2 = (2GM/r)1/2
　　従って、V2 = V1*1.414 ≒ 11.2km/sです。