■人工衛星の理論軌道の計算式について

　先の人工衛星の打上げシミュレーションプログラム "iEarth Satellite"においては、オイラー法およびルンゲ・クッタ法による数値計算により衛星の軌道を計算しています。
　ここでは水平方向の発射に限定して、人工衛星の軌道の理論式を示すとともに"iEarth Satellite"の改良版を紹介します。改良版では数値計算による軌跡に加えて、理論軌道も表示されます。


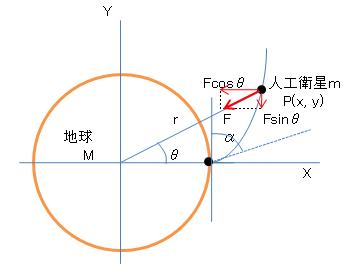
左図で、打上げ角α=0度の水平方向発射の場合を考えます。

ただし、途中までの計算式は任意の発射方向に適用できます。

人工衛星の軌道の理論式の導出

・人工衛星の軌道に関する運動方程式（２階の微分方程式）：
　　x"＝　-GMx/r3
　　y"＝　-GMy/r3
　　ここで、
　　　G　：　万有引力定数
　　　M　：　地球の質量
　　　r　：　地球の中心と人工衛星の距離、r2 = x2 + y2
　を初期条件［時刻t=0 で x=r0, y=0, 速度v=v0］で解きます。

・直交座標系で表現されたこれらの式を極座標系(r,θ)に変換します。両者の関係
　　x = rcosθ
　　y = rsinθ
　より、
　　x' = r'cosθ - rsinθθ'
    x" = r"cosθ - 2r'sinθθ' -rcosθ(θ')2 - rsinθθ"
　　y' = r'sinθ + rcosθθ'
    y" = r"sinθ + 2r'cosθθ' -rsinθ(θ')2 + rcosθθ"

・加速度の動径（ｒ）方向成分：Ar
　　Ar = x"cosθ + y"sinθ
　　　 = r" - r(θ')2
　加速度の方位角（θ）方向成分：Aθ
    Aθ = -x"sinθ + y"cosθ
　　　　= 2r'θ' + rθ"
        = (r2θ')'/r

・力の動径（ｒ）方向成分：Fr = -GMm/r2
　力の方位角（θ）方向成分：Fθ = 0

・従って、極座標系での運動方程式は
　　r" - r(θ')2 = -GM/r2　・・・(式１）
   (r2θ')'/r = 0
　後者の式より
　　r2θ' = c1  (c1: 積分定数）
　　mr2θ' = mc1
　左辺は角運動量(mrv)であり、これが一定であることから t=0 での初期値 r = r0, v = v0 を代入して
　（これ以降は打上げ角度α=0度の水平方向発射の場合に限定）
　  mr2θ' = mr0v0
　  r2θ' = r0v0　・・・(式２）

・(式２）のθ'を(式１）に代入すると、動径ｒ方向の２階の微分方程式が得られます。
　　r" -(r0v0)2/r3 + GM/r2 = 0

・変数の置換 u = 1/r を行ない、整理すると（途中の過程は省略）
　　d2u/dθ2 + u = 1/L 
    ここで、L = (r0v0)2/(GM)

・この解は
　　u = 1/r = Acos(θ+β) + 1/L   (A, β: 積分定数）
  θが0のときｒが最小（u が最大）となるように角度を設定すればβ＝0となるから
　　u = 1/r = Acos(θ) + 1/L
　　r = L / (1 + εcosθ）
　　ここで、 ε=AL　：離心率

・t=0で θ=0, r=r0 とすると
　　r0 = L / (1 + ε)  --> ε = L/r0 - 1
  となり、結局（打上げ角0度、すなわち水平方向に発射される）人工衛星の軌道方程式は
　　r = L / (1 + εcosθ）　　　・・・(式３）
　　　ここで、ε = L/r0 - 1
　　　　　　　L　= (r0v0)2/(GM)
  となります。この式は極座標での円錐曲線（二次曲線）を表しています。

末尾のシミュレーションプログラムで確認してください。

(注１）ε=0 すなわち L=r0 のときはｒ＝一定となり、円軌道となります。
　　　　このときの初期速度v0は
　　　　　(r0v0)2/(GM) = r0
        より、v0 = (GM/r0)1/2 : 第一宇宙速度です。
       また、ε<1 のときは楕円、ε=1 のときは放物線、ε>1 のときは双曲線となります。

(注２）任意の打上げ角度αに対する軌道方程式は次のとおりです。
　　　　　r = L / (1 + εcos(θ+β）)
　　　　　ここで、L　= (r0v0cosα)2/(GM)
　　　　　　　　　β = tan-1[L/(L-r0)・tanα]
　　　　　　　　　ε = (L-r0)/r0/cosβ
　　　　　　　
(注３）極座標系での運動方程式については、Wikipediaの「軌道（力学）」を参考にしました。