■車の数学（６）：　コーナリング時の遠心力による横滑りと浮上がり

　車がカーブを曲がるときには図のように遠心力：Fc が働き、車は外側に押し出されようとします。　車には遠心力も含めて次のような力が働きます。
　　・重量：　W = mg　　　　(m: 車の質量、　g: 重力加速度)
　　・遠心力：　Fc = mv2/r　　（v: 速度、　r: カーブ半径）
　　・回転中心に向かう摩擦力（最大）：　Ff = μW = μmg　（μ: 摩擦係数）
　　・走行方向の駆動力
　　・走行方向の抵抗力
　一定の速さで走行しているときには、走行方向の上記２つの力は釣り合っています。　ここでは、これら以外の力（走行方向に直角な方向の力）のバランスについて考えます。
centrifugal.jpg
（１）横滑り
　遠心力Fcが摩擦力Ffを越えると車の横滑りが発生します。限界速度は次のとおりです。
　　Fc = Ff
    mv2/r = μmg
    v2 = μgr
（２）浮上がり
　左車輪接地点の回りのモーメントMは
　　M = Fc・h - W・t/2　　　（ｔ：トレッド = 左右の車輪間距離）
　　  = mv2h/r - mgt/2
　この値が０以上になると車体が浮き上がろうとします。限界速度は次のとおりです。
　　mv2h/r = mgt/2
　　v2 = gtr/(2h)
（３）どちらが支配的か？
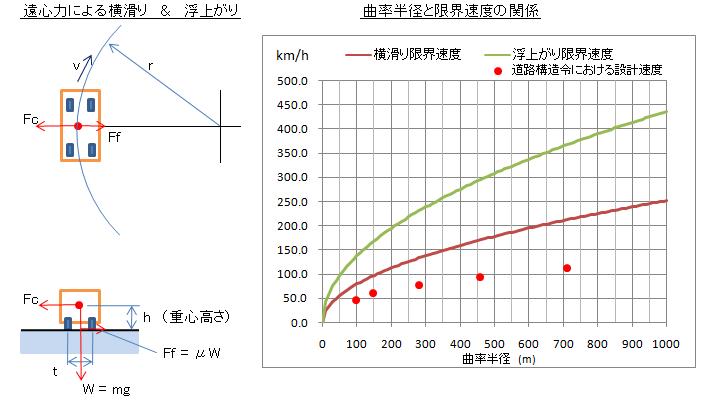
　一般的な車と道路面において、μ = 0.5、h = t/3 と仮定すると、
　　・横滑りに対して　：　v2 = μgr = 0.5gr
　　・浮上がりに対して：　v2 = gtr/(2h) = 1.5gr
であり、横滑りに対する限界速度の方が小さいことがわかります。
　上右図は曲率半径と横滑り・浮上がりの限界速度の関係を示します（但し、μ=0.5、h=t/3 の場合）。
　電車のようにレールにより横滑りを規制されており、また比較的に重心が高い乗り物では
浮上がり・転倒が重要な問題となります。
（４）道路構造令
　道路構造令第15条には道路の設計速度とそれに対する最小曲率半径を規定されています。
　その一部の値を上のグラフ中に赤丸で示します。
ホーム