■レンズの焦点距離の計算式

　凸レンズや凹レンズなどの球面レンズの焦点距離(f)については、近軸光線（注１）に限った次の近似式があります。


●近似式１（薄肉レンズに対する式）：
　　　f1 = 1/[(n-1) (1/r1 - 1/r2)]

●近似式２（レンズの厚さを考慮した式）：
　　　f2 = 1/[(n-1) (1/r1 - 1/r2) + (n-1)²d/(n r1 r2)]
　　ここで、
　　　ｎ：　レンズ材質の屈折率
　　　r1：　レンズ前面の曲率半径
　　　r2：　レンズ後面の曲率半径
　　　ｄ：　レンズの厚さ
　　(注）r1, r2 には凸、凹に応じて表のように正負があります。

曲率半径 ｒ1、ｒ2 の符号

レンズの種類	ｒ１の符号	ｒ２の符号
凸　凸	＋	−
凸　凹	＋	＋
凹　凸	−	−
凹　凹	−	＋

曲率中心が右側（レンズの向こう側）にある場合は＋、左側（レンズ手前）にある場合は− となります。


●焦点距離の厳密計算
　さて、ここではこれらの近似式に加えて、光軸に平行な光線がレンズの前面、後面で屈折して進行方向を変えて光軸と交わる点（焦点：F）を「光の屈折の法則」に沿って厳密に計算することによって焦点距離(f)を求める方法を紹介します。
レンズの焦点距離の計算（Excel）をクリックしてください。

焦点距離(f)は主点（注２）から焦点までの光軸に沿った距離ですが、簡易的にレンズ中心から焦点までの距離(f0)とすることがあります。ここではそれら両方の値を算出しています。

(注１）近軸光線とは光軸（レンズ中心軸）付近を通過する光線のことです。
(注２）主点とは入射光P0P1とレンズ通過後の光P2Fの延長線上の交点です。
(注３）Excelによる計算で片方が平面のレンズ（平凸など）の場合には平面の側の曲率半径を例えば１．E10とします。
(注４）近似式２による焦点距離の値は厳密計算によるものとよく一致します。

●（参考）厳密計算式（計算手順）
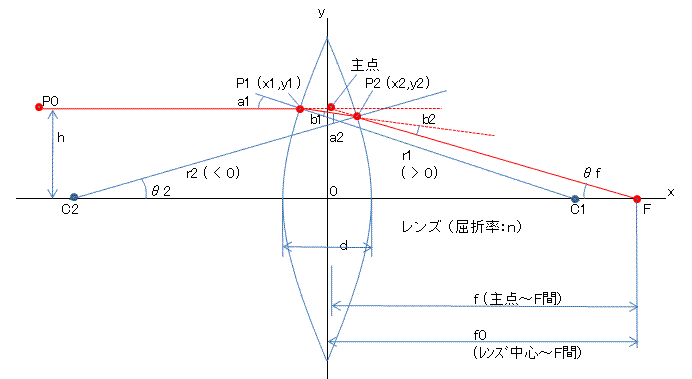
　上の凸レンズ（両凸）の図に沿って、焦点距離の計算手順を示します。
・x1 = (r1 - d/2) - sqrt(r12 - h2)　　(注）sqrt：平方根(ルート)
・y1 = h
・sin(a1) = h/r1
・sin(b1) = sin(a1)/n = h/r1/n　　(注）n = sin(a1)/sin(b1) より

　次に、点P1で屈折した光がレンズ後面（曲率半径r2）と交わる点P2を以下のようにして求めます。
・光の進路の式（直線）
　　y - y1 = -tan(a1-b1)(x - x1)
・レンズ後面の方程式（円）
　　(x - r2 - d/2)2 + y2 = r22
・直線の式を ｙ について解いて、円の式に代入すると
　　(x - r2 - d/2)2 + [y1 - tan(a1-b1)(x - x1)]2 = r22
・これを未知数ｘについて整理すると
　　Ax2 + Bx + C = 0
　　ここで、
　　　A = 1 + [tan(a1-b1)]2
　　　B = -r2 - d/2 - [y1 + x1tan(a1-b1)]tan(a1-b1)
　　　C = (-r2 - d/2)2 + [y1 + x1tan(a1-b1)]2 - r22
・この2次方程式を解くと、点P2のｘ座標（x2）が得られます。
　　x2 = [-B + sqrt(B2 - AC)] / A　　(注）凸の場合は２つの解のうち大きい方
　　(注）後面が凹のときは　x2 = [-B - sqrt(B2 - AC)] / A　（２つの解のうち小さい方）
・y2 = y1 - tan(a1-b1)(x2 - x1)
・sin(θ2) = y2/(-r2)
・a2 = a1 - b1 + θ2
・sin(b2) = n・sin(a2)
　　(注）sin(a2) > 1/nのときは後面で全反射するため、これ以降の計算はできません。
・θf = b2 - θ2

　従って、焦点距離は
・主点を基準にするときは
　　f = h/tan(θf)
・レンズ中心を基準にするときは
　　f0 = x2 + y2/tan(θf)
となります。
以上の式は、レンズ面の曲率半径r1、r2の符号を前記表のように約束すると、凹レンズや凸凹レンズに対しても成立します。