■折り紙で数学：　容器の容積を最大にするには

　折り紙は正方形の紙を折って動植物など種々の物の形を作る日本伝統の遊びです。折り紙の持つ幾何学的な性質から、数学の一分野としても研究されています。
　ここでは図のような正方形の紙から、
　　・底辺が正方形の直方体の容器　と
　　・底辺が正方形の４角錐の容器
を作るとき、その容積を最大にするには底辺をどのような大きさにすればいいか考えてみましょう。


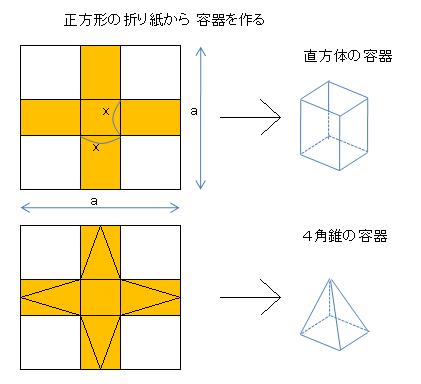
　紙の１辺の長さを a、底辺の１辺の長さを x とします。xを小さくすれば容器の高さが高くなり、逆にxを大きくすれば高さが低くなります。容積は底面の面積（ｘの２乗）と高さの積に比例しますので、最適なxの値がありそうです。

＜底辺が正方形の直方体の容器の場合＞

・底辺の１辺の長さを x とすると、容器の高さｈは(a-x)/2となります。
・従って容積Vは
　　V = x2(a-x)/2
・Vを最大にするｘ(0<x<a)は
　　dV/dx = x(a-x) -x2/2 = 0
　　x(2a-3x)/2 = 0
　より、x = 2a/3 が得られます。
・このときの容積は
　　V = 2a3/27
  となります。

＜底辺が正方形の４角錐の容器の場合＞

・底辺の１辺の長さを x とすると、容器の高さｈは
　　h = sqrt((a-x)2 - x2)/2   (注）sqrt:平方根の意
　となります。
・従って容積Vは
　　V = x2h/3
　　  = x2・sqrt(a(a-2x))/6
・Vを最大にするｘ(0<x<a/2)は
　　dV/dx = ax(2a-5x)/sqrt(a(a-2x))/6 = 0
　　ax(2a-5x) = 0
　より、x = 2a/5 が得られます。
・このときの容積は
　　V = 2a3/(75・sqrt(5))
  となります。

＜底辺が正方形の直方体の容器の場合で、4隅の切れ端部分で更に同様の容器を作ると…＞

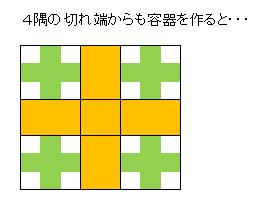
　底面が正方形の容器では上記のように x = 2a/3 のときに容積が最大(V0 = 2a3/27)になりました。
ここで4隅に残った部分（１辺が a/6）で同様の容器を作るとその小さな容器4個の容積は
　　V1 = V0・(1/6)3・4
更にここで各4隅に残った部分（１辺が a/62）で同様の容器を作るとその小さな容器4x4個の容積は
　　V2 = V1・(1/6)3・4 = V0・(1/6)6・42
これを無限に繰り返して、出来上がるすべての容器の容積を合計すると
　　Vsum = V0 + V1 + V2 + ・・・
　　　　 = V0 [ 1 + r + r2 + ・・・ ]
　　　　 = V0/(1 - r)
　　ここで  r = 4・(1/6)3
　∴ Vsum = 4a3/53