・回答者の内、男性の人数をM、女性の人数をF
・男女それぞれの中で、夏が最も好きと答えた人数をm、f
としたとき、男女全体(M+F)人について、夏が最も好きな人(m+f)の割合について考えます。
r1 = m/M
r2 = f /F
ra = (m + f)/(M + F)
とすると、全体の比 ra が r1 と r2 の間の値になることは容易に想像できますが、ここではそれを確認します。
r1 < r2 と仮定します。
● 数式による確認
ra - r1
= (m + f)/(M + F) - m/M
= [M(m + f) - m(M + F)]/[M(M + F)]
= (Mf - mF)/[M(M + F)]
= MF(f/F - m/M)/[M(M + F)]
= F(r2 - r1)/(M + F) > 0
ra - r2
= (m + f)/(M + F) - f/F
= [F(m + f) - f(M + F)]/[F(M + F)]
= (Fm - fM)/[F(M + F)]
= MF(m/M - f/F)/[F(M + F)]
= M(r1 - r2)/(M + F) < 0
∴ r1 < ra < r2
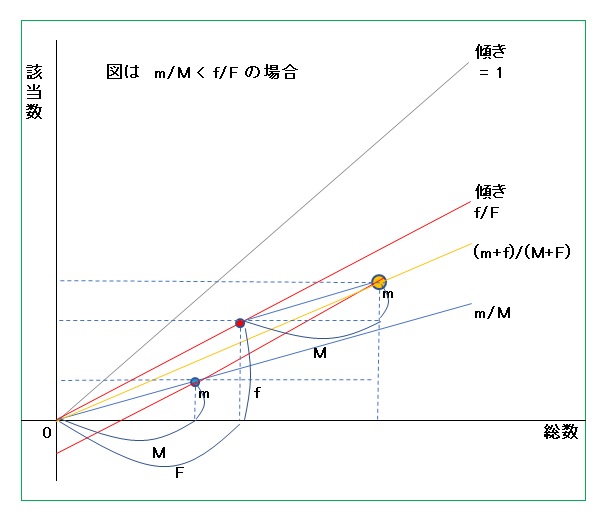
● グラフによる説明1
・横軸をデータ総数、縦軸を該当数とする座標平面上に点(M、m)、(F、f)をプロットする。
・原点(0,0)とそれぞれの点を結ぶ直線の傾きが比 r1 = m/M、r2 = f/F となる。
・点(F、f)を起点に、横方向にM、縦方向にmだけ行った点が全体数に対する該当点数となり、
この点と原点を結ぶ直線の傾きが比 ra = (m + f)/(M + F) である。
・これより、比 ra が r1 と r2 の間の値になることは明らかである。
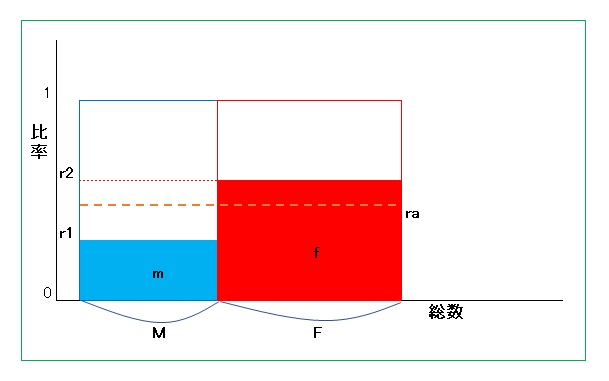
● グラフによる説明2
・図のように、データ総数に比例した幅の長方形M、Fを描く(高さは1)。
・各長方形において、該当比率 r1=m/M、r2=f/F の範囲を色付けする。
・色付けされた部分の面積は該当数 m、fに相当する。
・全体(M+F)に対する該当数は青、赤の面積の和で、これを横幅(M+F)の長方形にすると、
その高さは図中のオレンジ色のラインとなり、比 ra が r1 と r2 の間の値になることがわかる。
r1 = r2 の場合は当然 ra = r1 = r2 となります。