■音の出所はどこ？　[連立方程式の１解法]

ある点で発せられた音は四方八方へ同じ速度(音速：ｃ)で伝わります。周囲に複数個のマイクを設置し、各マイクに音が到達する時間を計ることにより、どこで音が出たかを知ることができます。

図のような2次元平面において、マイク１，２，３に音が到達した時刻をt1、t2、t3、音源Sの位置を(x0,y0)：未知数とします。

マイク１，２に音が到達する時間差(t2-t1)から次の式が成り立ちます。

　sqrt((x2-x0)^2+(y2-y0)^2) - sqrt((x1-x0)^2+(y1-y0)^2) = c(t2-t1)　…(式１)
　　ここで、sqrt : 平方根(ルート)
　　　　　　^2   : ２乗
　　を意味します。
同様に、マイク２，３に音が到達する時間差(t3-t2)から次の式が成り立ちます。

　sqrt((x3-x0)^2+(y3-y0)^2) - sqrt((x2-x0)^2+(y2-y0)^2) = c(t3-t2)　…(式２)

式１，２の連立方程式を解くことにより、音の発生場所(音源位置)(x0,y0)を求めることができます。 ちなみに、式１はマイク１の位置(x1,y1)およびマイク２の位置(x2,y2)を焦点とする双曲線１であり、式２はマイク２の位置(x2,y2)およびマイク３の位置(x3,y3)を焦点とする双曲線２です。

上記の連立方程式を解くことは、これら２つの双曲線の交点を求めることに相当します。交点は最大８個ありますが、時刻t1、t2、t3の大小関係を考慮することで通常はどれかに決まります。

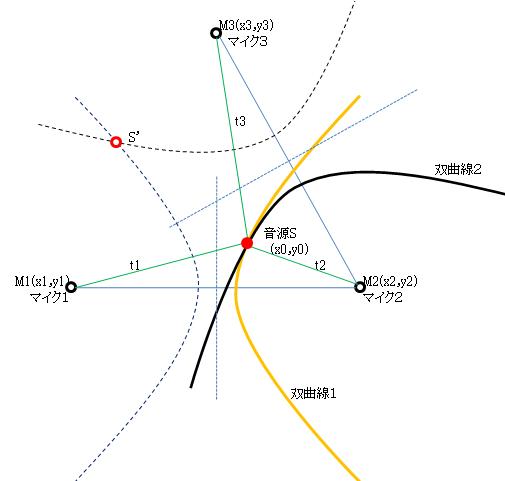
音の発生時刻をt0（未知数）とすると、前記の式１、式２は次のように分解できます。
　sqrt((x1-x0)^2 + (y1-y0)^2) = c(t1-t0)　…(式3.1)
　sqrt((x2-x0)^2 + (y2-y0)^2) = c(t2-t0)　…(式3.2)
　sqrt((x3-x0)^2 + (y3-y0)^2) = c(t3-t0)　…(式3.3)
ここで、音速cは既知とします（気温により決まる）。

式3.1〜式3.3を2乗すると、
　(x1-x0)^2 + (y1-y0)^2 = [c(t1-t0)]^2　…(式4.1)
　(x2-x0)^2 + (y2-y0)^2 = [c(t2-t0)]^2　…(式4.2)
　(x3-x0)^2 + (y3-y0)^2 = [c(t3-t0)]^2　…(式4.3)

式4.1から式4.2を引くと、
　(x1-x0)^2 + (y1-y0)^2 - (x2-x0)^2 - (y2-y0)^2 = [c(t1-t0)]^2 - [c(t2-t0)]^2
展開整理して、
　(x1^2+y1^2-x2^2-y2^2)-2x0(x1-x2)-2y0(y1-y2) = c^2(t1^2-t2^2)-2c^2t0(t1-t2)　…(式5.1)

同様に、式4.1から式4.3を引き、展開整理すると、
　(x1^2+y1^2-x3^2-y3^2)-2x0(x1-x3)-2y0(y1-y3) = c^2(t1^2-t3^2)-2c^2t0(t1-t3)　…(式5.2)

式5.1、式5.2を変形して、
　-2(y1-y2)y0+2c^2(t1-t2)t0 = c^2(t1^2-t2^2)-(x1^2+y1^2-x2^2-y2^2)+2(x1-x2)x0　…(式5.1a)
　-2(y1-y3)y0+2c^2(t1-t3)t0 = c^2(t1^2-t3^2)-(x1^2+y1^2-x3^2-y3^2)+2(x1-x3)x0　…(式5.2a)

ここで、
　a1=-2(y1-y2),  b1=2c^2(t1-t2),  c1=c^2(t1^2-t2^2)-(x1^2+y1^2-x2^2-y2^2),  d1=2(x1-x2)
　a2=-2(y1-y3),  b2=2c^2(t1-t3),  c2=c^2(t1^2-t3^2)-(x1^2+y1^2-x3^2-y3^2),  d2=2(x1-x3)
とおくと、式5.1a、式5.2aは
　a1y0 + b1t0 = c1 + d1x0　…(式5.1b)
　a2y0 + b2t0 = c2 + d2x0　…(式5.2b)
となります。

これをy0, t0に関する連立方程式と考えて解くと、
　y0 = Ax0 + B　…(式6.1)
　t0 = Cx0 + D　…(式6.2)
　ここで、
　　A = (b2d1-b1d2)/(a1b2-a2b1),   B = (b2c1-b1c2)/(a1b2-a2b1)
　　C = (a1d2-a2d1)/(a1b2-a2b1),   D = (a1c2-a2c1)/(a1b2-a2b1)

この y0、t0を式4.1に代入すると、x0に関する次の2次方程式が得られます。
　[x1-x0]^2 + [y1-(Ax0+B)]^2 = [c[t1-(Cx0+D)]]^2

x0について整理すると、
　Ex0^2 + Fx0 + G = 0
　ここで、
　　E = 1 + A^2 - c^2C^2　　　　　　　　（小文字cと大文字Cに注意）
　　F = -2x1 - 2(y1-B)A + 2c^2(t1-D)C
　　G = x1^2 + (y1-B)^2 - c^2(t1-D)^2

これを解くと音の発生位置x0が得られ、更に式6.1よりy0が求められます。
　x0 = [-F ± sqrt(F^2 - 4EG)]/(2E)　　（但し、F^2 - 4EG ≧ 0 のとき）

（注）x0に関する2次方程式からは通常解が２個得られますが、このx0を式6.2に代入して
　　　得られるt0について、t0 < t1, t2, t3 を満たさないものは除外します。