これらを適当に組み合わせると、ジグソーパズルのようにスキマなく敷き詰めることができます。
これは「秋山の4面体タイル定理」と呼ばれています。 東海大学の秋山仁先生によって数年前に証明されました。
・図1は正4面体0-1-2-3の3D図(3次元図、アイソメ図)と、それを上から見た図(上面図)です。
図中の赤い曲線は4頂点を通る切り込み線です。ここでは底面には切り込みを入れていません。
・図2は切り込み線によって3側面を色分けしたものです。
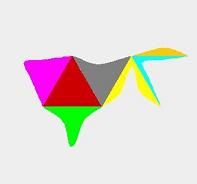
・切り込み線にハサミを入れて、これを平面に展開すると図3のようになります(赤色の3角形は底面)。
・このような形状を数個作成し(図4)、うまく組み合わせると図5のようにスキマなく敷き詰めることができます。
| 手 順 | 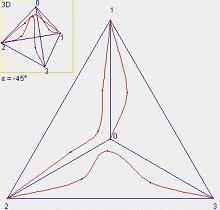 |
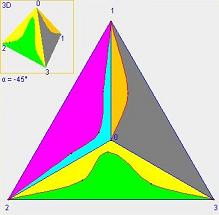 |
| 図1.正4面体と切り込み線 | 図2.切り込み線によって色分け | |
 |
 |
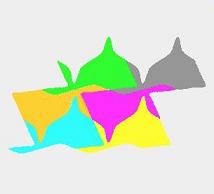 |
| 図3.平面展開図 | 図4.コピーを数個作成 | 図5.スキマなく敷き詰める |
このように展開図のコピーをジグソーパズルのようにくぼんだ所に出っ張ったところをピッタリはめ込み,平面を隙間もなく重なりもなく敷き詰めることができるとき、その展開図は平面充填図形と呼ばれます。
正4面体を作って色々と試してみると面白いと思います。
「秋山の4面体タイル定理」のわかりやすい説明がNHKの次のサイトに掲載されていますので、興味のある方はどうぞ。
NHK高校講座 数学基礎 第19回 芸術と数学