「1本の矢なら折れるが、3本の矢なら折れない」
と戒めた「三本の矢」の逸話(三矢の訓: さんしのおしえ)は、あまりにも有名ですが、同じような話は世界中に残されているようです。
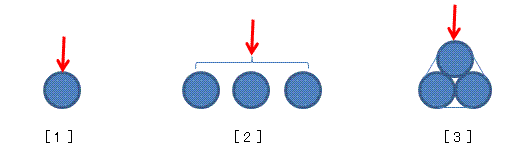
これに関して、以前の記事で、(下図[3]のモデルに対して)
1本の矢より3本の矢の方が折れにくい(強い)ことは明らかですが、では一体何倍の強度なのでしょうか。
単純には3倍と思われますが、実は構造材に負荷を加えたときの変形や破壊について研究する学問である「材料力学」の理論をもとに計算すると何と 1本の矢の約5倍の強度(折れにくさ) になることがわかります。
また「たわみにくさ」については、1本の矢の約11倍 にもなるのです。
うまく組み合わせる(協力する)ことによって単純に3倍でなく、それ以上の力を発揮する訳です。
と紹介しました。
これは3本の矢を強固に束ねて一体化した場合(図[3])の計算結果をもとに記しています。
これに対して先日ある方から、これは間違いである旨のご指摘を頂きました。
「3本の矢」の話は3本を接着しない場合であり、3本を強固に束ねた(接着して一体物として挙動する)としての計算は間違いであると。
そこで「三本の矢」の逸話をもとに再度整理してみました。
●「三本の矢」(Wikipediaを参照)
毛利元就が書いた三子教訓状を基にした逸話で
3人の息子の前で、元就はまず1本の矢を取って折って見せるが、
続いて矢を3本束ねて折ろうとするが、これは折る事ができなかった。
そして元就は、「1本の矢では簡単に折れるが、3本纏めると容易に折れないので、
3人がよく結束して毛利家を守って欲しい」と告げた。
というものであるが、史実であるか疑わしい。
教訓状には「三本の矢」については記述がない。
3本を具体的にどのように束ねるかについても詳細不明であり、またこの故事の内容は時代とともに変遷している。
−>三本の矢の真実 (ここには「毛利元就の矢の話」の変遷がまとめられている)
●「3本の矢」の計算モデル
(1)3本を強固に束ねた場合
以前紹介したとおり。
(2)単純に3本を束ねた場合(接着なしでそれぞれ独立に変形)
・断面2次モーメントは単純に1本の場合の3倍
・それぞれの断面係数は1本の場合と同じで、外力を均等に分担するので応力は1/3。
−>従って、たわみにくさ、強度とも1本の場合の3倍。
となり、話は単純である。
−>九州大学資料「複合化の世界〜その科学と思想〜」 (ここには「糊なし3本矢(毛利元就の故事)」とある)
(3)実際の状態
3本を束ねた場合のたわみ量、強度(折れにくさ)はその束ね方(固定方法)により、
完全に接着した場合とそれぞれが独立して挙動する場合の中間の状態になると考えられる。
しかし、これを数式化することはちょっと困難である。
●当方の個人的希望的見解
3本の矢を手で握ったとき、それ程には強く握られないので接着なしとする方が現実的か?
しかし、「3本の矢」の逸話には、3本を具体的にどのように束ねるかについての記述が見当たらない。
3本の矢を束ねて、その両端を極めて力強く握って曲げるときは、
両端部は一体化され、3倍以上の強さになる。
3本で3倍になるのは当たり前すぎる。
皆が協力(結束)すれば3倍以上の力を発揮できることもあると解釈したい。
「3本の矢」の話は皆で協力することの重要性を説いたものである。
矢の束ね方(固定方法)についてはそれぞれ計算モデル化する各人の自由な考え方に任せて、
「このようにモデル化するとこうなる」ということで十分ではないだろうか。