■アプローチタイルの盛り上がり量の検討（複数タイルの影響）

　道路 ～ 門扉 ～ 玄関へと続く我が家のアプローチは、正方形のタイルを若干のすき間を設けて規則正しく並べ、すき間に目地材を流し込んで施工されていますが、数年前から一部のタイルの盛り上がりが立つようになりました。
　（注）現在、盛り上がりの高さは10～14ｍｍに達しています（下の写真参照、近々改修予定）。


　先に、タイルまたは目地材の温度（熱）や水分（雨水）などによる膨張が盛り上がりの原因と仮定し、前後各1枚のタイルに着目して盛り上がり量を検討した結果を示しましたが、ここでは影響範囲を拡大し、前後複数枚のタイル、目地材の膨張による盛り上がりについて考察しています。

＜前回の概要＞
　前回はアプローチのタイルと目地の２スパン分を図のようにモデル化しました。　１スパンの長さが a です。



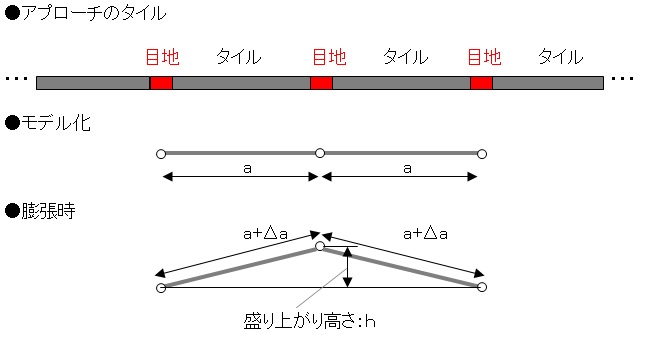
　タイルあるいは目地材（の片方または双方）がΔa だけ膨張し、それが単純にタイルの盛り上がりとなると仮定すると、その高さｈ は以下のようになりました。
　　h = (2aΔa)^1/2

　a = 100 mm, Δa = 0.1 mm ならば、h ≒ 4.5 mm,
　a = 100 mm, Δa = 0.2 mm ならば、h ≒ 6.3 mm,
　a = 100 mm, Δa = 0.5 mm ならば、h ≒ 10 mm です。

＜今回の検討＞
　今回はこれを拡張し、盛り上がり頂部の前後各ｎ枚の（タイル＋目地材）が同量Δa だけ膨張した場合について検討します。
　簡単化のため、以下ｎ＝３に限定して記します。

　先ず、下図にようにタイルが直線的に盛り上がる場合は前回紹介した量の単純にｎ（＝３）倍になります。



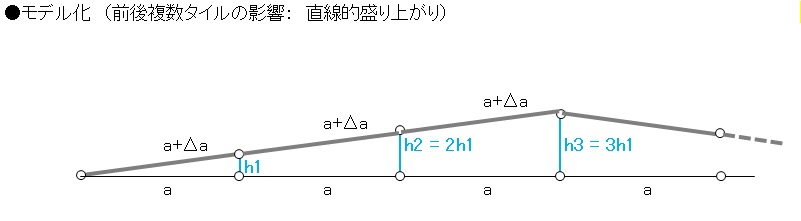
　　h = n(2aΔa)^1/2

　a = 100 mm, Δa = 0.1 mm, n = 3 ならば、h ≒ 13.4 mm です。

　次に、タイルが徐々にせりあがって大きな山となる時の盛り上がり高さについて検討します（下図参照）。
　前掲の写真はこれに近い状況を示しています。



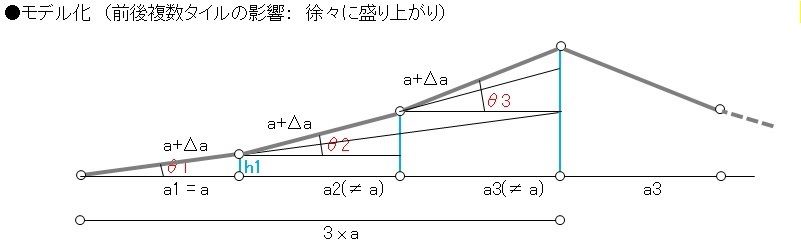
　各タイルの傾き角をθ1＝θ、θ2＝2θ、θ3＝3θとすると、
　　(a+Δa)cosθ + (a+Δa)cos2θ + (a+Δa)cos3θ = 3a
　　(a+Δa)[cosθ + cos2θ + cos3θ] = 3a

　ここで、cosθ ≒ 1 - θ²/2, T = θ²　と置いて整理すると、
　　(a+Δa)[3 - 7T] = 3a
　微小項 ΔaTを省略すると、
　　T = (3/7)(Δa/a)
　　θ = [(3/7)(Δa/a)]^1/2
　　h = (a+Δa)[θ + 2θ + 3θ] = 6aθ　　　　（Δaは無視）

　∴　h = [(108/7)aΔa]^1/2

　が得られます。

　a = 100 mm, Δa = 0.1 mm , n = 3 ならば、h ≒ 12.5 mm で、結果的に前述の直線的盛り上がりの場合の13.4mmと大差ありませんが、わずか１スパン 0.1mmの膨張が10mmを超える盛り上がりとなって表れることがわかります。

　タイルと地面との間の固着が不十分で、また亀裂や割れ目のある状態であればこのような現象が発生してもおかしくはありません。

（参考）タイルの傾き角（a = 100 mm, Δa = 0.1 mm , n = 3 の場合の計算値）
　　・直線的に盛り上がる場合：　θ = 2.6°
　　・徐々にせりあがる場合　：　θ1 = 1.2°, θ2 = 2.4°, θ3 = 3.6°