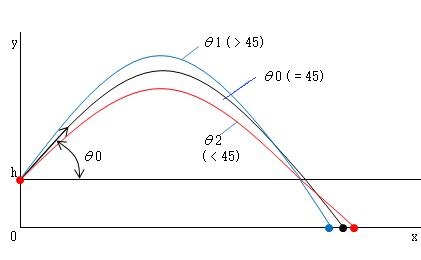
では、どの程度の角度で投げれば最も遠くまで到達するのでしょうか。 微分方程式の復習を兼ねて考えてみましょう。
図のように、地上hの高さから水平に対して角度θの方向に投げた物体の運動は、下記運動方程式で表されます。 これを解くと、最適な角度が求められます。h=0の場合はθ=45度のときに水平距離が最大になることがわかります。
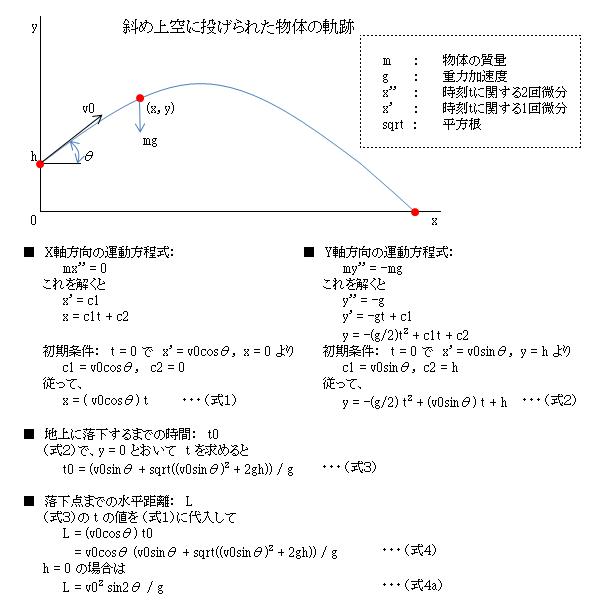
・人間が通常ボール投げをするときは45度方向には投げません。 これはあまり角度をつけると力が入らず、従って速度が出せないからだと思われます。 ・ピッチングマシンや大砲のように、機械的に物体を放出させるものにおいては45度方向が飛距離最大になります。 ・hが0でないときは45度より若干小さい角度で最大になります。 このことは数値計算でも容易に確認できますが、詳しくは ボールをより遠くまで投げるには(その2)をご覧ください。 しかし、断崖絶壁の上から海上に投げるような場合を除けばその角度のずれは無視できます。 ・θ=44度と46度では、44度の方が遠くまで飛びます。 これはボールが最高点から落下して再度y=hになる点が同一となり、そこでの速度ベクトルの方向がθと 等しくなることから理解できます。