■音律と音階の科学（１）：　２つの音の不協和度とは

　小方厚著「音律と音階の科学」（講談社発行）は、ドレミファ・・・の音階がどのようにして生まれたかについて数学的な観点から大変興味深く書かれています。
　その中で私が特に感銘を受けたものは「音の不協和」に関する各種グラフです。　協和・不協和とは２つ（以上）の音を同時に鳴らした時に心地よく聞こえるか否かを示すものであり、全員が不協和と感じれば不協和度 D（dis） = 1、誰もが不協和と感じなければ D = 0 となります。

　さて、「音律と音階の科学」では次の２つのグラフ：
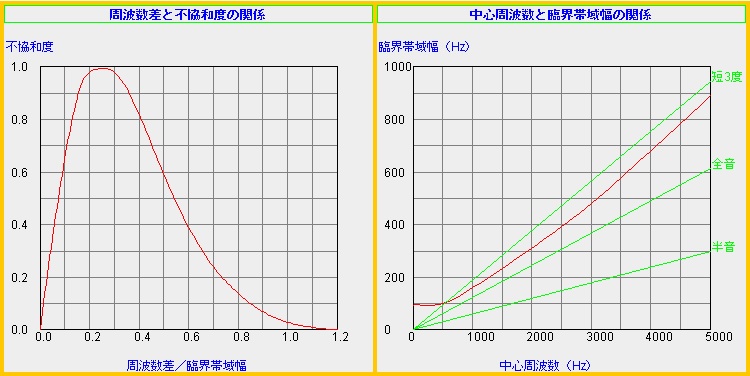
　（a）不協和曲線（下図左）：　周波数差／臨界帯域幅と不協和度の関係を示す。
　（b）臨界帯域幅（下図右）：　中心周波数と臨界帯域幅の関係を示す。
を出発点にして、
　（1）２つの純音の不協和曲線：　根音の周波数をパラメータにした、周波数比と不協和度の関係
　（2）２つの楽音の不協和曲線：　倍音を考慮した２つの楽音（楽器の音）の周波数比と不協和度の関係
　（3）３重音（３和音）の不協和曲面：　根音に対する２つの周波数比と不協和度の関係
を計算した結果がグラフで示されています。

　（a）、（b）の２つのグラフを元に、（1）〜（3）のグラフを作図するアプレットを作成したので順に紹介します。
　先ず、今回は元になる（a）、（b）の２つのグラフの説明から始めます。

　２つの純音（基本周波数のみで倍音を持たない音）を同時に聴いたときの不協和度D（dis）を、周波数差の関数として表したものです。しかし横軸に生の周波数差を取ると根音（２音のうち低い方の音）の高低によってそれぞれ異なった曲線となるため、次項の「臨界帯域幅」で割った値を横軸に取ります。
　この曲線をここでは次式で表現します。
　　dis = Fa (�冉/b)
　　　　�凾�：　周波数差　f2-f1
　　　　ｂ　：　臨界帯域幅

２つの音を同時に聴いたとき、
（１）２音の周波数の差が小さい時は、２音の平均周波数の単音と２音の周波数差を周波数とする”うなり”が重なって聞こえます。
（２）周波数差を大きくしていくとうなりは消え、２音の平均周波数を持つ単音がゴロゴロした感じで聞こえます。
（３）更に差を広げると２つの音が認識できますが、ゴロゴロ感は残ります。
（４）更に差を広げるとゴロゴロ感も消えて、２つの独立した純音が聞こえます。

うなり領域とゴロゴロ感がある（１）〜（３）の領域を合わせたものが「臨界帯域幅」（ｂ）です。
ここではこれを次式で表現します。
　　b = Fb (f1)
　　　　f1：　根音（２音のうち低い方の音）の周波数

図中には「半音」、「全音」、「短３度」の音程が周波数によって変化する様子も示しています。「半音」、「全音」のラインがいずれも臨界帯域幅のラインより下方にあるので、例えば「ドとレ（全音）」を同時に聴くと心地よくなく、また「ドとミ（長３度）」は心地よく聴こえることがわかります。

(注１）グラフ（a）、（b）の曲線の値は「音律と音階の科学」の中の図から数値を読み取ったものを使用しています。
(注２）「半音」、「全音」、「短３度」の各ラインの式は次のとおりです。
　　　　半音：　�冉 = f1 [2^1/12 - 1]
　　　　全音：　�冉 = f1 [2^2/12 - 1]
　　　　短３度（３半音）：　�冉 = f1 [2^3/12 - 1]

(注３)　2020/11/20: グラフ(a)、(b)をJavaアプレット表示から、直接画像表示に変更しました。
　　　　Javaアプレットが実行できないブラウザに対応するため。