・回答者の内、男性の人数をM、女性の人数をF
・男女それぞれの中で、夏が最も好きと答えた人数をm、f
としたとき、男女全体(M+F)で夏が最も好きな人(m+f)の割合は男性での割合と女性での割合の中間の値になることを示しました。
ここでは、これを一般化して、N個のグループについての比率の平均値について考えます。
各グループのデータ数 A1、A2、A3、・・・での該当数を a1、a2、a3、・・・としたとき、全データ中の該当数の比率について考えます。
r1 = a1/A1
r2 = a2/A2
r3 = a3/A3
・
・
ra = (a1 + a2 + a3 + ・・・)/(A1 + A2 + A3 + ・・・)
とすると、全体の比 ra が ri(i=1,2,3,...)の最小値と最大値の間の値になること示します。
ここでは、前回示したグラフによる方法2で説明します。
● グラフによる説明
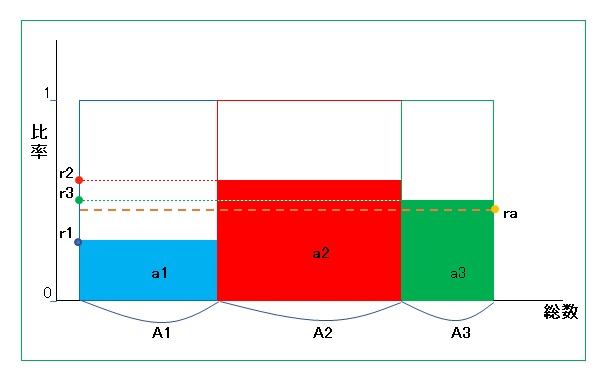
説明上、3グループの場合で話を進めます。
・図のように、データ総数に比例した幅の長方形A1、A2、A3を描く(高さは1)。
・各長方形において、該当比率 r1、r2、r3 の範囲を色付けする。
・色付けされた部分の面積は該当数 a1、a2、a3 に相当する。
・全体(A1+A2+A3)に対する該当数はこれら色付けされた面積の和で、これを横幅(A1+A2+A3)の長方形にすると、
その高さは図中のオレンジ色のラインとなり、比 ra が r1、r2、r3 の最大値と最小値の間の値になることは一目瞭然である。
r1 = r2 = r3 ・・・の場合は当然 ra = r1 = r2 = r3 ・・・となります。