●整然と並んだ螺旋
ひまわりの種を見ると、螺旋(らせん)状に整然と並んでいます。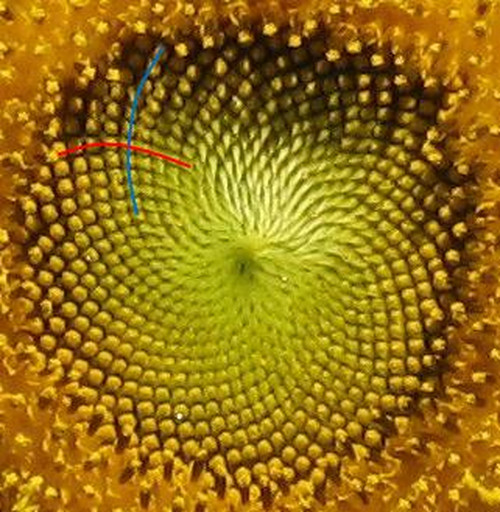
上の写真では青の螺旋が34本、赤の螺旋が55本確認できます。 更に詳しく観察すると、21本や89本の螺旋も存在します。
21、34、55、89 などはいずれもフィボナッチ数列に含まれる数字です。
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ・・・
●螺旋の乱れ
しかし、実際にはすべてのひまわりの種がこのような法則に沿っているわけではないようです。次の写真は先日庭で採取したものですが、赤で示す右向き螺旋は76本、緑で示す左向き螺旋は47本で、これらはいずれもフィボナッチ数列には含まれてません。
よく観察すると、中心部から外周に向かう途中で螺旋が枝分かれしている箇所が見受けられます(下方の拡大図)。 これにより、フィボナッチ数列から外れてしまうのです。
ところで、76、47という数値は
76 = 21 + 55
47 = 13 + 34
であり、いずれもフィボナッチ数列の「ある項」と「その次の次の項」の和になっています。 偶然でしょうか。 それとも何かあるのでしょうか。

赤、緑それぞれ螺旋10本毎に線を描いている。

全体写真の右下部分の拡大図: 赤、緑の螺旋が途中で枝分かれしている。