■フィボナッチ数列（３）：　黄金比と黄金角

　フィボナッチ数列の一般項の計算式には黄金比 φ：

　　φ　＝　[ 1 + sqrt(5) ]/2 （ = 1.618･･･）

が含まれています。

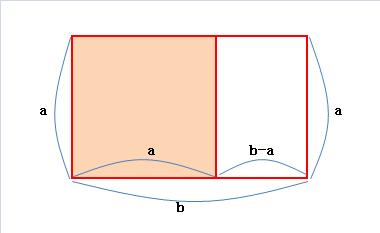
　図のような長方形（ a < b ）において、正方形（ a x a ）を切り取り、残った長方形の縦横比が最初の長方形の縦横比と等しい時、

　　a / b　＝　（ b - a ）/ a

　ここで、x = b/a（ > 0 ）と置くと、

　　1/x = x - 1
　　x² - x - 1 = 0　　　・・・　（式１）

　これより、

　　 x = [ 1 + sqrt(5) ]/2

が得られ、これが黄金比 φとなります。

　黄金比は最も美しい比率と呼ばれ、各種カードやディスプレイの縦横比もこれに近い値になっているものが多くあります。


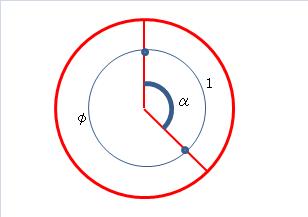
　黄金角 α は円周360度を１：φの比に分割した時の（小さい方の）角度です。

黄金角　α	＝　360 x 1 / ( 1 + φ )	＝　360 / φ2
	＝　137.507764･･･ °

　（注）　（式１）より−＞ φ² - φ - 1 = 0　−＞ φ² ＝ φ + 1

　黄金角はひまわりの種の配列計算式の中に出てきます。