■フィボナッチ数列（２）：　ひまわりの種の配列を描く

　ひまわりの種を見ると、らせん（螺旋）状に整然と並んでいます。

　写真では青のらせんが34本、赤のらせんが55本確認できます。　更に詳しく観察すると、21本や89本のらせんも存在します。
　21、34、55、89 などはいずれもフィボナッチ数列に含まれる数字です。

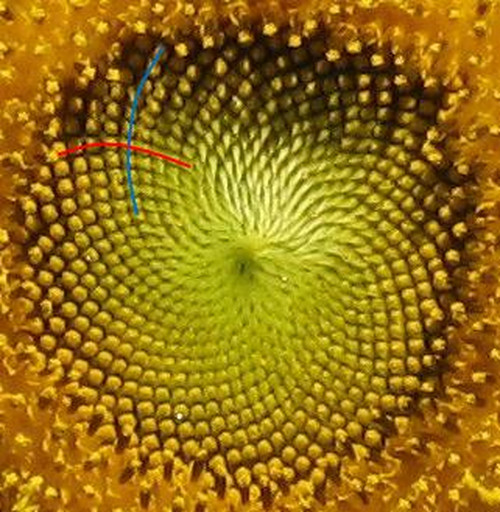
　ここでは、ひまわりの種の配列を描くプログラムを紹介します。

　種の数、らせん表示の種類などを変えて、ひまわりの種の配列（並び）の神秘を眺めて下さい。

　・計算スピードを変更できる。
　　　最小にすると約1秒毎に種が増える様子が確認できる。
　　　最大にすると瞬時に計算終了。
　　　計算中もスピード変更可能。
　・図の拡大、縮小、移動ができる。
　・各種の表示オプションがある。
　　　デモ表示も可能。
　・種の数を変更したら、「計算＆表示」ボタンをクリックする。




[ 計算式 ]

　ひまわりの花（頭花）の中心を原点とする直交座標系における種の位置（x, y）：
　　　x = a・t・cos [ (α/180)πt ]
　　　y = a・t・sin [ (α/180)πt ]
　　ここで、
　　　a　：　任意の定数
　　　t　：　パラメータ（媒介変数）
　　　α　：　黄金角　＝　360/ （ 1 + φ ）　＝　360/ φ²　（ =　137.507764･･･°）
　　　φ　：　黄金比　＝　[ 1 + sqrt(5) ]/2 （ = 1.618･･･）

　パラメータ ｔ に自然数 1, 2, 3, ･･･ を順に代入して（x, y）値をプロットしていく。

（注）　（x, y）の計算式において、
　　　　(α/180)π = α (π/180) = 2π/ φ²　（ ≒ 2.4 ）

　　であり、これは黄金角をラジアン単位で表したものである。