■アプローチタイルの盛り上がり量の検討（全タイルの影響）

　道路 ～ 門扉 ～ 玄関へと続く我が家のアプローチは、正方形のタイルを若干のすき間を設けて規則正しく並べ、すき間に目地材を流し込んで施工されていますが、数年前からアプローチ中央付近のタイルの盛り上がりが目立つようになりました。
　（注）盛り上がりの高さは10～14ｍｍに達している（下の写真参照）。


　以前、タイルまたは目地材の温度（熱）や水分（雨水）などによる膨張が盛り上がりの原因と仮定し、アプローチ中央部の前後各1枚あるいは複数枚（3枚）のタイルと目地材の膨張による盛り上がりについて検討し、その結果を示しました。

　ここでは、更に影響範囲を拡大し、アプローチ全長（門扉～玄関ポーチ階段手前までの、長手方向タイル約50枚分の約５ｍ）の膨張を考えます（道路から門扉までは除外）。

　アプローチの両端は門扉を支える門柱・ブロック塀と玄関前の階段であり、ここでタイルの長手方向の変位は拘束されているものとし、各タイルのひずみ（熱などによる膨張）がアプローチ全長の中央で一気に盛り上がりとなって現れているものと考えます。

　以下、アプローチ端から中央部までの膨張とそれによる盛り上がりについて検討します。

a	：　1スパンの長さ
n	：　スパン数（アプローチ端から中央までのタイル数）
Δa	：　膨張量
h	：　盛り上がり高さ
θ	：　盛り上がり角度

１．全膨張を中央タイル1枚で吸収する場合


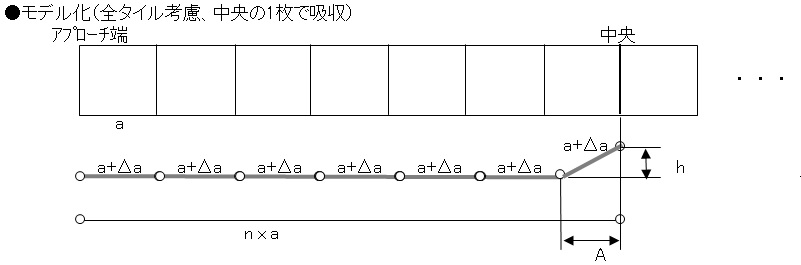
　　A = na - (n-1)(a+Δa) = a - (n-1)Δa
　　h² = (a+Δa)² - A² = 2naΔa　　（注）2次の微小項を省略、以下同様

　∴ h = (2naΔa)^1/2

２．全膨張を中央タイル3枚で吸収する場合（直線的盛り上がり）


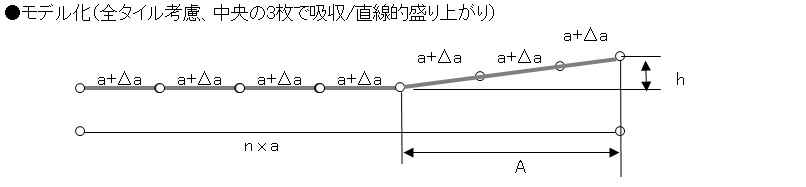
　　A = na - (n-3)(a+Δa) = 3a - (n-3)Δa
　　h² = [3(a+Δa)]² - A² = 6naΔa

　∴ h = (6naΔa)^1/2

３．全膨張を中央タイル3枚で吸収する場合（徐々に盛り上がり）


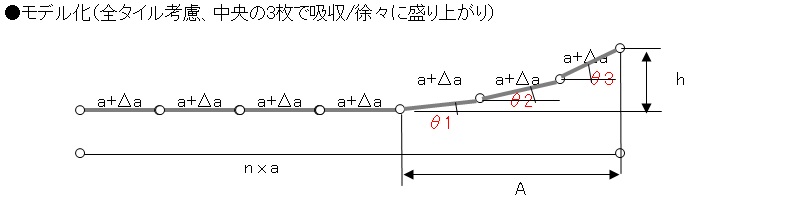
　　A = na - (n-3)(a+Δa) = 3a - (n-3)Δa

　一方、各タイルの傾き角をθ1＝θ、θ2＝2θ、θ3＝3θとすると、
　　A = (a+Δa)[cosθ + cos2θ + cos3θ]
　　　= (a+Δa)(3 - 7θ²)　　　（注）cosθ = 1 - θ²/2

　これより、
　　3a - (n-3)Δa = (a+Δa)(3 - 7θ²)
　　θ = [(n/7)(Δa/a)]^1/2
　　h = (a+Δa)[θ + 2θ + 3θ] = 6aθ　

　∴　h = [(36n/7)aΔa]^1/2

● タイル盛り上がり高さの計算式まとめ
　いずれのケースでも盛り上がり高さはタイル寸法、タイルの膨張量の平方根に比例。

膨張範囲	盛り上がり範囲	盛り上がり形状	計算式
中央部付近	前後各1枚	－	h = [2aΔa]1/2
	前後各3枚	直線的	h = 3[2aΔa]1/2
		徐々に	h = [(108/7)aΔa]1/2
全タイル	前後各1枚	－	h = [2naΔa]1/2
	前後各3枚	直線的	h = [6naΔa]1/2
		徐々に	h = [(36n/7)aΔa]1/2

● タイル盛り上がり高さの数値計算例
　　a = 100mm, Δa = 0.008mm, n = 25枚

膨張範囲	盛り上がり範囲	盛り上がり形状	盛り上がり高さ
中央部付近	前後各1枚	－	1.3 mm
	前後各3枚	直線的	3.8 mm
		徐々に	3.5 mm
全タイル	前後各1枚	－	6.3 mm
	前後各3枚	直線的	10.9 mm
		徐々に	10.1 mm

　全タイルの膨張を考慮したモデルでは盛り上がりが 10ｍｍ前後となり、実際と近い値が得られます。