角度増分値を黄金角( ≒ 137.507764 度)に等しくすると、ひまわりの種の配列となり、平面上に点(種)がほぼ均等に分布していることがわかります。
角度増分値を色々変えて、パターンを確認してみましょう。
平面上の点分布の均一度を測る目安として、ここでは2つの指標:
(1)各点から最も近い点までの距離の平均値: da ・・・ 大きいほど均一
(2)各点から最も近い点までの距離のバラツキ(標準偏差): ds ・・・ 小さいほど均一
を考えます。
画面内の左側に表示される da、ds が距離の平均値とバラツキです。
・・・ 以下、点(種)の数=1000のとき ・・・
角度増分値を1〜359度の範囲で変化させて、距離の平均値 (da)、バラツキ (ds) を求めた結果をグラフにすると、次のようになります。
角度増分値=黄金角のとき(図中の赤丸)、da = 100.009、ds = 36.062 となり、値 da はグラフ中の最大値(≒ 103)に近い値になっています。
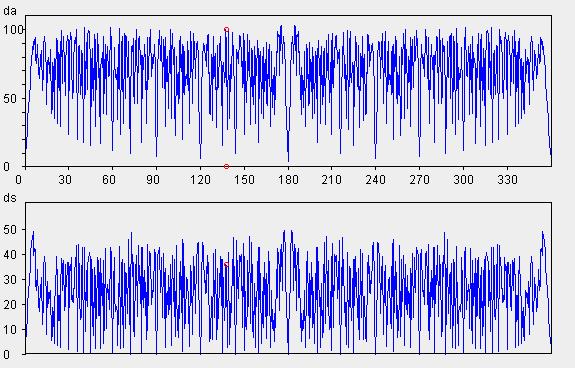
値 da が最大値に近い値となる角度増分値は数多く存在しますが、例えば角度増分値=86度では、da = 100.365、ds = 40.203 となって、バラツキを示す値 ds が黄金角の場合に比べて若干大きくなっています。
両者の点分布を示すと下図のように、全体図では大差がありませんが、中心部を拡大してみると黄金角の時の分布の方が均一であることが分かります。 86度の時は、らせん方向の間隔が小さく、それと直交する方向(円周方向)の間隔が大きくなっています。
● 角度増分値=黄金角の場合


● 角度増分値=86度の場合

