■2次元不規則分布データの補間の例
〜 色彩工学におけるマクアダム楕円の補間 〜
米国の物理学者マクアダム(1910-1998)はxy色度図上の25点(色)について等色実験を行い、その色と区別がつかない範囲をその点を中心とした楕円で示しました。 これがマクアダム楕円(あるいはマクアダム標準偏差楕円)です。
ここでは、既知の25個のマクアダム楕円データを元に、任意点(色度)での楕円の大きさ(長半径、短半径)、傾きを1次補間により算出する手順について記述しています。
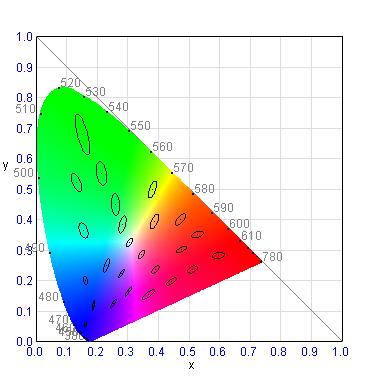
●xy色度図におけるマクアダム楕円
図の25個の楕円がマクアダム楕円である。
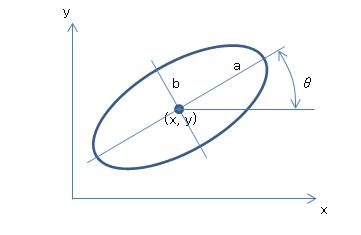
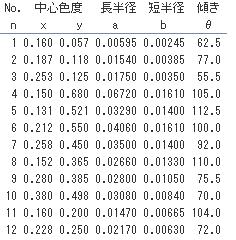
●マクアダム楕円のデータ形式
25個のマクアダム楕円について、中心座標(x, y)、長半径(a)、短半径(b)、長軸の傾き(θ)が与えられている。
●3角形領域への分割
25個のマクアダム楕円の中心点を結んで図のような3角形領域に分割する(全37領域)。
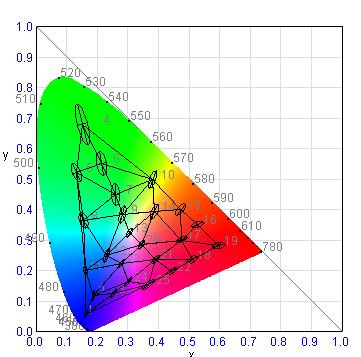
補間できる範囲は上図のいずれかの3角形の内部にある点で、概ね25個の楕円中心点の凸包(とつほう)の内部である。
●指示点が含まれる3角形領域の決定
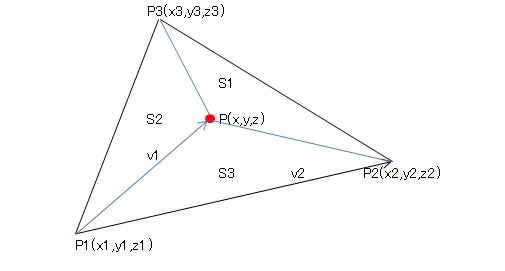
任意に指示された補間点P(x, y)がどの3角形領域に含まれているかは、ベクトルの外積を利用して決定する。
・ベクトル v1 = P1P と v2 = P1P2 の外積のz成分
・ベクトル v1 = P2P と v2 = P2P3 の外積のz成分
・ベクトル v1 = P3P と v2 = P3P1 の外積のz成分
がすべて負または0であれば、点P(x, y)は3角形P1P2P3の内部(線上を含む)にある。
(注)ベクトル v1(v1x, v1y, 0) と v2(v2x, v2y, 0) の外積のz成分は(v1x*v2y - v1y*v2x)である。
●補間(方法1)
点P(x, y)を含む3角形P1P2P3の頂点座標(xi, yi, zi)から、点Pのz座標を1次補間により求める(ここで z は長半径、短半径、傾きなどの属性値)。
z = Ax + By + C
と置いて、3頂点の座標を代入する。
z1 = Ax1 + By1 + C
z2 = Ax2 + By2 + C
z3 = Ax3 + By3 + C
この連立方程式を解いて、係数A,B,Cを求めれば、点Pでのz値が計算できる。
●補間(方法2: 面積座標による)
上記の1次補間は面積座標による下記方法と同等であることが容易に証明できる(次項参照)。
・点Pと3角形P1P2P3の関係を示す図において、点Pの回りの小3角形の面積をS1,S2,S3とする。
・点Pでのz値は次式で計算できる。
z = (S1z1 + S2z2 + S3z3) / S
ここで、
S1 = [ (x3-x2)(y-y2) - (x-x2)(y3-y2) ] / 2
S2 = [ (x1-x3)(y-y3) - (x-x3)(y1-y3) ] / 2
S3 = [ (x2-x1)(y-y1) - (x-x1)(y2-y1) ] / 2
S = S1+S2+S3: 3角形P1P2P3の面積
尚、例えば S3はベクトル v2 = P1P2 と v1 = P1P の外積のz成分の1/2である。
この方法はベクトルの外積による内外判定の途中結果を利用できるので便利である。
●2つの補間方法が同等であることの証明

CIE XYZ表色系
CIE XYZ表色系(17):マクアダム楕円の補間
(マクアダム楕円表示補間プログラム)
点群の凸包を求める
ホーム

